Administering Insulin To Diabetic Patients Assignment Sample

Introduction

Get free samples written by our Top-Notch subject experts for taking online Assignment Help services.

In this report paper, three tasks will be performed on the basis of the different performance of the PID controller for the different Glucose concentration and the different rate of delivery of the Insulin for the diabetes patient. This is performed to maintain the proper steady state for the system.

2.0 Discussion

Task 1

In this part different parameters are normally used for proper design of the appropriate type step test. For this a test model is undersigned for the proper values estimation from the FOPTD model. This will derive the different positive type step test. In this case, proper analysis will be derived for the different negative and the different positive tests. This is done for 63.2% input. The values are declared by the proper Simulation result. In this case, the magnitude starts from the 0.5 value. The PID model will show the different values for the positive test and the negative test.  This will declare the proper IAE value for the given condition. At the end of the results, validity is checked properly and the values are declared according to the validity of the simulation result. The graph of the result will represent the concentration of the Glucose for the different positive step changes and the different negative step changes. For this calculation transfer function is used. The values of the delta Y are represented by the different steps and the ultimate result is declared by this process.  This graph is accurate for the Glucose concentration of the patient. This will help to determine the actual performance of the PID controller.

Figure 1: Design of FOPTD model and incomplete fraction method in Mat Lab

(Source: self made in Mat Lab)

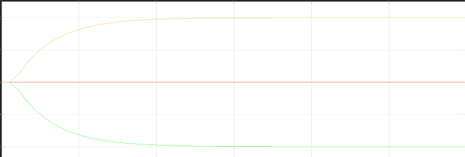
Figure 2:  Result of FOPTD model and incomplete fraction method in Mat Lab

(Source: self-made in Mat Lab)

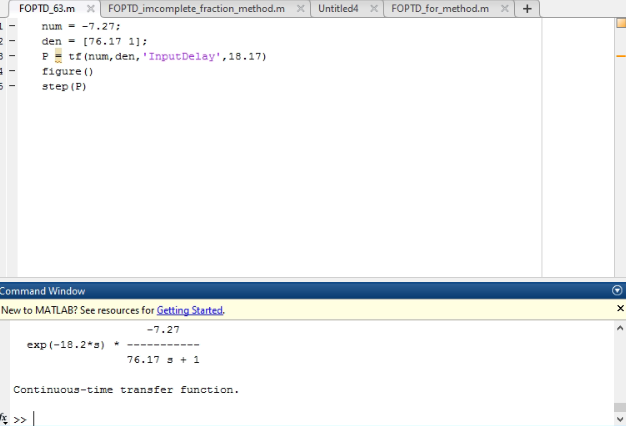
Figure 3 : FOPTD model for 63.3% Method

(Source: self made in MAT LAb)

Figure 4: FOPTD model result for 63.3% Method

(Source: self made in MAT LAb)

For 63.2% method:

Positive Step test

Step Size	DELTA(y)	Y_63.2%	K	t	t	tD	ISE
0.5	-2.275	-2.22	-7.432	90	72	19	6.654
1	-5.322	-3.19	-7.762	100	82	18	14.354
1.5	-10.145	-8.32	-7.265	100	82	18	18.678
Average			-7.646		79	18.43

 

Negative Step Test

Step Size	DELTA(y)	Y_63.2%	K	t	t	tD	ISE
-0.5	2.465	-2.45	-7.098	94	75	19	6.654
-1	5.933	-3.69	-7.143	85	88	19	12.354
-1.5	11.498	-8.93	-7.875	85	82	18	19.678
Average			-7.339		71.76	18.43
Over all Average			-7.395		77.32	18.93

 For fraction incomplete method

Positive Step test

Step Size	Y_35.3%	Y_85.3%	t1	t2	t	tD	ISE
0.5	-1.275	-3.22	54	120	72	25.56	6.654
1	-2.322	-3.19	55	140	79	18.35	14.354
1.5	-3.145	-7.32	56	165	64	18.76	18.678
Average					78	18.43

 

Negative Step Test

Step Size	Y_35.3%	Y_85.3%	t1	t2	t	tD	ISE
-0.5	2.465	-2.45	-7.098	94	75	19	6.654
-1	5.933	-3.69	-7.143	85	88	19	12.354
-1.5	11.498	-8.93	-7.875	85	82	18	19.678
Average			-7.339		71.76	18.43
Over all Average			-7.395		77.32	18.93

 

 

Task 2

In this part, the different tuning performances of the PID are declared by the proper Ziegler Nichols Method. This is the most popular method for proper tuning of the PID controller. This model will start from the gain value 0 and after some time, the proper proportional gain will be increased gradually and the final value of the Kp, Ki and Kd will be declared by this process. In this simulation result, the proper value o0f the Kp during the instability situation is called sq the K_Max. In this model the proper value of the K_c will be declared. For this case a Mat Lab Script is generated for the system. This will declare the total three figures. First inked is for the root Locus and second one is the declaration of the result. The last figure will declare the proper value of the Kp,Kd,Ki. This section is the proper combination of the different goals estimated result. In this case, the value of the Kcu and the value of the Pu are already declared. The graph is estimated by the proper maintenance of the given value. A huge noise value is observed during the delivery rate of the insulin.  This performance is represented by the Graph.

Task 3

In this part a PID controller is designed which will be implemented on the proper patient. This will declare the proper rate of the insulin and glucose on the body of the patient. This will show the proper oscillation for the patient during the delivery of the glucose and the insulin.  In this case, the different proportional, m derivative and the other intrigue value are computed for the proper output generation for the patient. This will declare the proper steady state of the controller. For this case, in this simulation model a negative feedback is normally used for the declaration of the different value of the concentration of the Glucose. In this case, a model is designed which will help to decrease the noisy output for the insulin delivery type rate. This section will help to declare the proper expected result for the system.  For this reason, the filter will help to decrease the effect of the noise in the output of the simulation result.  This section will help to declare the proper design and the proper maintenance of the PID controller in the given situation. 

Task 4

 The main objective of this part is to determine the proper optimum type tuning process for the insulin delivery process.  For this reason, the proper Ziegler Nichol method is used to determine the actual tuning value of the systems.  The proper equation for this is IE = ∫^∞₀ e(t) dt. This will declare the proper absolute type integral error for this system. In this part, the proper representations of the different graphs will be declared. According to the different results it is observed that the IAE value for the PID controller is far better than the other system. In this case v, drawback is observed for this system. The output for this system is a little bit noisy. For this case, suppressed type PI controllers are also used and different graphs are represented by this system. This graph is represented by the Mat Lab simulation result.

3.0 Conclusion

In this part, different tasks will be represented. For this reason, different simulation results are represented by the system. In the first part, the proper mat lab Script is designed for the FOPTD model. In the second section, a proper tuning method is observed which Ziegler Nichols is for the system. This section will be delivered for the running of the controller.  In this case, the value will start from 0.5. Different simulation results will declare the proper performance of the PID controller for the given situation. At the end of this a proper declaration is provided to choose the efficient controller for this system.

Reference List

Journal

Farahmand, B., Dehghani, M. and Vafamand, N., 2019. Fuzzy model-based controller for blood glucose control in type 1 diabetes: An LMI approach. Biomedical Signal Processing and Control, 54, p.101627.

Rahmanian, F., Dehghani, M., Karimaghaee, P., Mohammadi, M. and Abolpour, R., 2021. Hardware-in-the-loop control of glucose in diabetic patients based on nonlinear time-varying blood glucose model. Biomedical Signal Processing and Control, 66, p.102467.

Wang, V. and Awais, Q., 2020. Diabetes Millitus Control Exogenous Insulin Infusion: A Review. Pakistan Journal of Engineering and Technology, 3(1), pp.18-23.

Adedigba, A.P., Zubair, A.R., Aibinu, A.M., Adeshina, S.A., Okubadejo, O. and Folorunso, T.A., 2019, December. Towards the Development of Intelligent Insulin Injection Controller For Diabetic Patients. In 2019 15th International Conference on Electronics, Computer and Computation (ICECCO) (pp. 1-6). IEEE.

Rahmanian, F., Asemani, M.H., Dehghani, M. and Mobayen, S., 2022. Robust dynamic output feedback control of blood glucose level in diabetic rat with robust descriptor Kalman filter. Biomedical Signal Processing and Control, 71, p.103088.

Farman, M., Saleem, M.U., Ahmed, M.O. and Ahmad, A., 2018. Stability analysis and control of the glucose insulin glucagon system in humans. Chinese Journal of Physics, 56(4), pp.1